
 Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,2 м. Найдите длину тени человека в метрах.
Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,2 м. Найдите длину тени человека в метрах.
Рассмотрим рисунок:
BD - человек
AE - высота фонаря
ED - расстояние от фонаря до человека
DC - длина тени человека
Рассмотрим треугольники ACE и BCD.
∠C - общий
∠AEC=∠BDC=90° (это прямые углы)
Следовательно, по
первому признаку подобия треугольников, эти треугольники
подобны.
Тогда:
AE/BD=EC/DC
AE/BD=(ED+DC)/DC
7,2/1,8=(6+DC)/DC
4=6/DC+1
3=6/DC
DC=6/3=2
Ответ: 2 м.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=2:3, KM=14.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=2:3, KM=14.
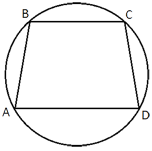 Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
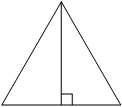 Высота равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.
Высота равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.
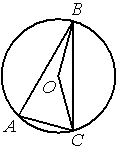 Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Комментарии:
(2016-10-29 11:49:48) Администратор: Кристина, (6+DC)/DC=6/DC+DC/DC=6/DC+1
(2016-10-29 11:21:57) Кристина: как из выражения 6+DC/DC у нас получается 6/DC+1?