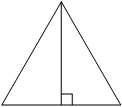
Высота равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.
В равностороннем треугольнике все стороны равны, пусть стороны равны "а".
По свойству равностороннего треугольника высота так же является и медианой, т.е. делит сторону по полам.
Треугольники, которые образует высота, являются прямоугольными.
Следовательно, к ним можно применить теорему Пифагора:
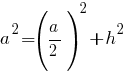
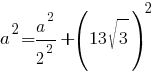
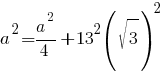
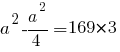
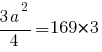
3a2=4*169*3 |:3
a2=4*169
a2=676
a=√676=26
Ответ: 26
Поделитесь решением
Присоединяйтесь к нам...
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=108°. Ответ дайте в градусах.
Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=19° и ∠ACB=160°. Найдите угол DCB. Ответ дайте в градусах.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AMD.
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: