В треугольнике ABC угол C прямой, BC=8, cosB=0,8. Найдите AB.
По
определению косинуса, cosB=ВС/АВ=8/АВ=0,8.
АВ=8/0,8=10.
Ответ: АВ=10.
Поделитесь решением
Присоединяйтесь к нам...
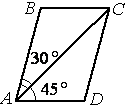Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Найдите площадь треугольника, изображённого на рисунке.
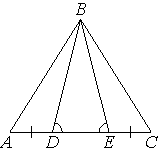На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: