
 В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
Рассмотрим треугольник АОВ. Этот треугольник
равнобедренный, т.к. ОА и ОВ - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OAB=/OBA.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=55°
Ответ: /OCD=55°.
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
 Углы при одном из оснований трапеции равны 48° и 42°, а отрезки, соединяющие середины противоположных сторон трапеции равны 6 и 3. Найдите основания трапеции.
Углы при одном из оснований трапеции равны 48° и 42°, а отрезки, соединяющие середины противоположных сторон трапеции равны 6 и 3. Найдите основания трапеции.
 Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=15, AC=25.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=15, AC=25.
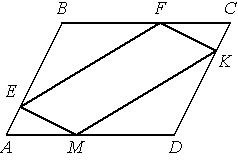 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Комментарии:
(2017-02-14 20:09:10) Администратор: Катя, была проблема у хостера, проблема устранена. Сейчас все читаемо?
(2017-02-14 14:50:46) Катя: не грузит решение, все в знаках вопроса. что такое??