
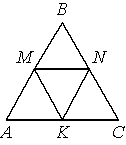
 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
Рассмотрим треугольники AMK, MBN и NCK.
/A=/B=/C (по
свойству равностороннего треугольника).
AM=MB=BN=NC=CK=KA (по условию задачи).
Следовательно, треугольники AMK, MBN и NCK равны (по
первому признаку).
Отсюда следует, что MN=MK=KM => треугольник MNK - равносторонний (
по определению).
Поделитесь решением
Присоединяйтесь к нам...
Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите диаметр описанной окружности треугольника ABC.
 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
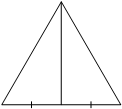 Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
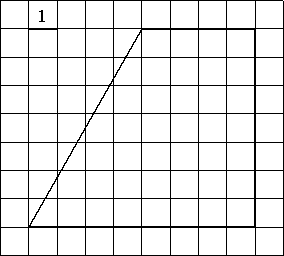 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
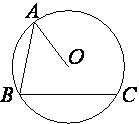 Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=43° и ∠OAB=13°. Найдите угол BCO. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=43° и ∠OAB=13°. Найдите угол BCO. Ответ дайте в градусах.
Комментарии:
(2018-03-11 14:39:19) Администратор: Антон, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2018-03-05 15:44:45) антон: ДАно Mk, NK,KM- средние линии MN:NK:MK PТреугол Abc = 45 Найти AB BC AC
(2016-02-14 18:07:07) Администратор: Виктория, да, все верно. У этой задачи может быть несколько доказательств.
(2016-02-11 20:25:46) Виктория: Я рассуждала так - т.к. МN,NK,KM - средние линии треугольника АВС, То каждая из них равна половине параллельной стороны. А т.к. каждая сторона треугольника АВС делится точками пополам по условию, то все отрезки равны MN=AK=KC=MK=BN=NC=KN=MB=MA, следовательно треугольник MNK равносторонний. Скажите, пожалуйста, правильное ли доказательство?
(2015-05-26 11:00:33) Микитикитакинакипукидуки: Артур, я с тобой полностью согласна
(2015-05-21 18:35:36) Артур: это самый лучший сайт в мире