
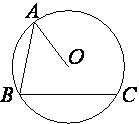
 Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=43° и ∠OAB=13°. Найдите угол BCO. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=43° и ∠OAB=13°. Найдите угол BCO. Ответ дайте в градусах.
 Проведем отрезки CO и продолжим отрезок AO до отрезка BC, пересечение обозначим буквой E (как показано на рисунке).
Проведем отрезки CO и продолжим отрезок AO до отрезка BC, пересечение обозначим буквой E (как показано на рисунке).
Рассмотрим треугольник ABE. По
теореме о сумме углов треугольника запишем:
180°=∠OAB+∠ABC+∠BEA
180°=13°+43°+∠BEA
∠BEA=180°-13°-43°=124°
Смежный этому углу ∠OEC=180°-∠BEA=180°-124°=56° (запомним это)
Угол ABC является
вписанным углом, следовательно градусная мера дуги, на которую он опирается, вдвое больше (по
теореме о вписанном угле), т.е. градусная мера дуги AC равна 43°*2=86°
Угол АОС является
центральным и, соответственно, равен градусной мере дуги, на которую опирается. А опирается он на дугу AC, следовательно ∠AOC=86°
Смежный этому углу ∠COE=180°-∠AOC=180°-86°=94°
Рассмотрим треугольник OCE.
По
теореме о сумме углов треугольника запишем:
180°=∠OEC+∠COE+∠OCE
Вспомнив то, что запомнили ранее...
180°=56°+94°+∠OCE
∠OCE=180°-56°-94°=30°
∠OCE и есть искомый угол BCO.
Ответ: ∠BCO=30°
Поделитесь решением
Присоединяйтесь к нам...
 Прямые m и n параллельны. Найдите ∠3, если ∠1=6°, ∠2=101°. Ответ дайте в градусах.
Прямые m и n параллельны. Найдите ∠3, если ∠1=6°, ∠2=101°. Ответ дайте в градусах.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CKD.
 Радиус вписанной в квадрат окружности равен 14√
Радиус вписанной в квадрат окружности равен 14√
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC.
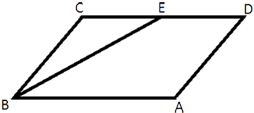 Площадь параллелограмма
ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
Площадь параллелограмма
ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
Комментарии: