
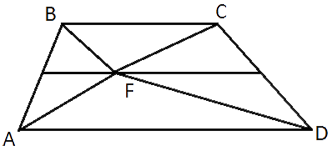 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
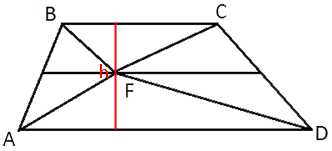 Проведем через точку F
высоту
трапеции h.
Проведем через точку F
высоту
трапеции h.
Высота h делится точкой F пополам, т.к. располагается на
средней линии, а средняя линия делит стороны трапеции пополам.
Таким образом получается, что высота обоих треугольников равна h/2.
Площадь треугольника равна половине произведения высоты на основание треугольника.
Площадь трапеции равна произведению полусуммы оснований на высоту.
SBFC=(h/2)*BC/2
SAFD=(h/2)*AD/2
SBFC+SAFD=(h/2)*BC/2+(h/2)*AD/2=(h/2)(BC+AD)/2=(h*(BC+AD)/2)/2=SABCD/2
Поделитесь решением
Присоединяйтесь к нам...
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
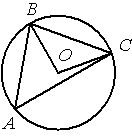 Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
 Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
 Площадь равнобедренного треугольника равна 144√
Площадь равнобедренного треугольника равна 144√
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.
Комментарии: