
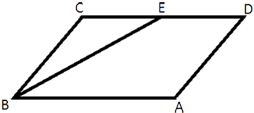 Площадь параллелограмма
ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
Площадь параллелограмма
ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
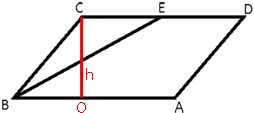 Проведем высоту
параллелограмма CO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Проведем высоту
параллелограмма CO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Sparal=AB*h=30
А площадь
трапеции равна произведению полусуммы оснований на высоту.
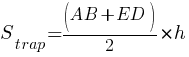
ED=DC/2 (по условию задачи).
DC=AB (по
свойству параллелограмма).
Следовательно ED=AB/2.
Тогда:
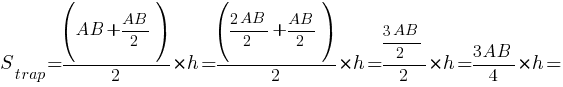
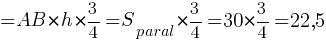
Ответ: 22,5
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C равен 90°, AC=6, tgA=2√
В треугольнике ABC угол C равен 90°, AC=6, tgA=2√
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 155°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 155°. Найдите угол C. Ответ дайте в градусах.
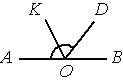 Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
 В треугольнике ABC угол C прямой, BC=6, cosB=0,3. Найдите AB.
В треугольнике ABC угол C прямой, BC=6, cosB=0,3. Найдите AB.
 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.
Комментарии:
(2017-10-10 09:50:50) Администратор: Илья, AB+AB/2=(2AB)/2+AB/2=(3AB)/2
(2017-10-09 09:37:18) Илья: Я не понял только одно, где вы взяли цифру \"3\" когда подставляли в формулу?
(2017-02-08 23:51:36) Администратор: Алена, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-02-08 12:33:24) Алена: В параллелограме ABCD AE биссектриса угла А. Стороны параллелограмма АВ и ВС относятся как 4/9. АЕ пересекают диагональ ВД в точке К. Найти отношение ВК/КД