
 В треугольнике ABC угол C прямой, BC=6, cosB=0,3. Найдите AB.
В треугольнике ABC угол C прямой, BC=6, cosB=0,3. Найдите AB.
По
определению косинуса cosB=BC/AB => AB=BC/cosB=6/0,3=20.
Ответ: AB=20.
Поделитесь решением
Присоединяйтесь к нам...
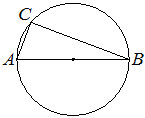 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если
угол BAC равен 74°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если
угол BAC равен 74°. Ответ дайте в градусах.
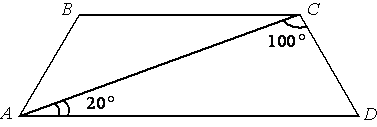 Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
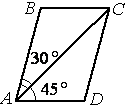 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 163°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 163°. Найдите угол C. Ответ дайте в градусах.
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника ABC.
Комментарии: