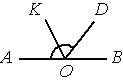
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
∠AOD=180°-∠DOB=180°-64°=116° (так как ∠AOB - развернутый, т.е. равен 180°).
Так как OK - биссектриса, то ∠DOK=∠AOD/2=116°/2=58°
Ответ: 58
Поделитесь решением
Присоединяйтесь к нам...
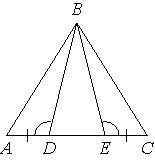На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
Какие из следующих утверждений верны?
1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
2) Площадь трапеции равна произведению основания трапеции на высоту.
3) Треугольника со сторонами 1, 2, 4 не существует.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
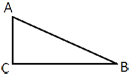Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 39.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: