
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ638 –Є–Ј 1087 |
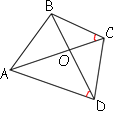 –Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABCD —Г–≥–ї—Л BCA –Є BDA —А–∞–≤–љ—Л. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —Г–≥–ї—Л ABD –Є ACD —В–∞–Ї–ґ–µ —А–∞–≤–љ—Л.
–Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABCD —Г–≥–ї—Л BCA –Є BDA —А–∞–≤–љ—Л. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —Г–≥–ї—Л ABD –Є ACD —В–∞–Ї–ґ–µ —А–∞–≤–љ—Л.
–Т–∞—А–Є–∞–љ—В 1
∠BCA –Є ∠BDA –Њ–њ–Є—А–∞—О—В—Б—П –љ–∞ –Њ—В—А–µ–Ј AB –Є —А–∞–≤–љ—Л –і—А—Г–≥ –і—А—Г–≥—Г.
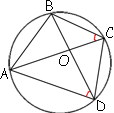 –Ч–љ–∞—З–Є—В –Љ—Л –Љ–Њ–ґ–µ–Љ –њ—А–Њ–≤–µ—Б—В–Є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М —З–µ—А–µ–Ј —В–Њ—З–Ї–Є AB –Є –≤–µ—А—И–Є–љ—Л —Н—В–Є—Е —Г–≥–ї–Њ–≤. –≠—В–Є —Г–≥–ї—Л –Њ–Ї–∞–ґ—Г—В—Б—П
–≤–њ–Є—Б–∞–љ–љ—Л–Љ–Є –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, –Њ–њ–Є—А–∞—О—Й–Є–Љ–Є—Б—П –љ–∞ –Њ–і–љ—Г –і—Г–≥—Г.
–Ч–љ–∞—З–Є—В –Љ—Л –Љ–Њ–ґ–µ–Љ –њ—А–Њ–≤–µ—Б—В–Є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М —З–µ—А–µ–Ј —В–Њ—З–Ї–Є AB –Є –≤–µ—А—И–Є–љ—Л —Н—В–Є—Е —Г–≥–ї–Њ–≤. –≠—В–Є —Г–≥–ї—Л –Њ–Ї–∞–ґ—Г—В—Б—П
–≤–њ–Є—Б–∞–љ–љ—Л–Љ–Є –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, –Њ–њ–Є—А–∞—О—Й–Є–Љ–Є—Б—П –љ–∞ –Њ–і–љ—Г –і—Г–≥—Г.
–Я–Њ–ї—Г—З–Є—В—Б—П, —З—В–Њ –Љ—Л –Њ–њ–Є—Б–∞–ї–Є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –≤–Њ–Ї—А—Г–≥ —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ —Г–≥–ї—Л ABD –Є ACD —В–Њ–ґ–µ —П–≤–ї—П—О—В—Б—П
–≤–њ–Є—Б–∞–љ–љ—Л–Љ–Є –Є –Њ–њ–Є—А–∞—О—Й–Є–Љ–Є—Б—П –љ–∞ –Њ–і–љ—Г –Є —В—Г –ґ–µ –і—Г–≥—Г, —В.–µ., –Є—Б–њ–Њ–ї—М–Ј—Г—П
—В–µ–Њ—А–µ–Љ—Г –Њ –≤–њ–Є—Б–∞–љ–љ–Њ–Љ —Г–≥–ї–µ, –њ–Њ–ї—Г—З–∞–µ–Љ, —З—В–Њ –Њ–љ–Є —А–∞–≤–љ—Л –і—А—Г–≥ –і—А—Г–≥—Г .
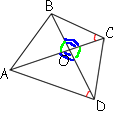 –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є OBC –Є OAD.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є OBC –Є OAD.–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
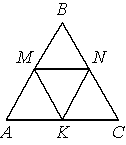 –Т —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —В–Њ—З–Ї–Є M, N, K вАФ —Б–µ—А–µ–і–Є–љ—Л —Б—В–Њ—А–Њ–љ –Р–Т, –Т–°, –°–Р —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –ТMKN вАФ —А–Њ–Љ–±.
–Т —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —В–Њ—З–Ї–Є M, N, K вАФ —Б–µ—А–µ–і–Є–љ—Л —Б—В–Њ—А–Њ–љ –Р–Т, –Т–°, –°–Р —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –ТMKN вАФ —А–Њ–Љ–±.
 –°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 26, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
–°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 26, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
 –Э–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –њ–Њ —А–∞–Ј–љ—Л–µ —Б—В–Њ—А–Њ–љ—Л –Њ—В –і–Є–∞–Љ–µ—В—А–∞ AB –≤–Ј—П—В—Л —В–Њ—З–Ї–Є M –Є N. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ ∠NBA=36¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї NMB. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Э–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –њ–Њ —А–∞–Ј–љ—Л–µ —Б—В–Њ—А–Њ–љ—Л –Њ—В –і–Є–∞–Љ–µ—В—А–∞ AB –≤–Ј—П—В—Л —В–Њ—З–Ї–Є M –Є N. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ ∠NBA=36¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї NMB. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Ш–Ј –≤–µ—А—И–Є–љ—Л –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ C —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –≤—Л—Б–Њ—В–∞ CP. –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BCP, —А–∞–≤–µ–љ 5 —Б–Љ, —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ ABC —А–∞–≤–µ–љ 2,4. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Ш–Ј –≤–µ—А—И–Є–љ—Л –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ C —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –≤—Л—Б–Њ—В–∞ CP. –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BCP, —А–∞–≤–µ–љ 5 —Б–Љ, —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ ABC —А–∞–≤–µ–љ 2,4. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
 –І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Я—А—П–Љ—Л–µ AB –Є CD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, BK=18, DK=9, BC=16. –Э–∞–є–і–Є—В–µ AD.
–І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Я—А—П–Љ—Л–µ AB –Є CD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, BK=18, DK=9, BC=16. –Э–∞–є–і–Є—В–µ AD.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2018-04-13 20:04:15) –Љ–∞—И–∞: —Б–њ–∞—Б–Є–±–Њ
(2017-03-09 20:00:07) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –У–µ–љ—А–Є—Е, –њ–Њ–ґ–∞–ї—Г–є—Б—В–∞, –Њ–±—А–∞—Й–∞–є—В–µ—Б—М. –Ъ—Б—В–∞—В–Є, –Т–∞—И –≤–Њ–њ—А–Њ—Б –Њ—З–µ–љ—М –њ—А–∞–≤–Є–ї—М–љ—Л–є.
(2017-03-07 17:42:44) –У–µ–љ—А–Є—Е: –Ф–∞, –≤—Б–µ –≥—А–∞–Љ–Њ—В–љ–Њ) —Б–њ–∞—Б–Є–±–Њ –±–Њ–ї—М—И–Њ–µ)
(2017-03-06 22:58:18) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –У–µ–љ—А–Є—Е, –Љ–Њ–ґ–љ–Њ –і–Њ–Ї–∞–Ј–∞—В—М –Њ—В –Њ–±—А–∞—В–љ–Њ–≥–Њ. –Э–∞–њ—А–Є–Љ–µ—А, —Н—В–Є –і–≤–∞ —Г–≥–ї–∞ —П–≤–ї—П—О—В—Б—П –≤–њ–Є—Б–∞–љ–љ—Л–Љ–Є –і–ї—П —А–∞–Ј–љ—Л—Е –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є. –Э–Њ –њ—А–Є —Н—В–Њ–Љ –≥—А–∞–і—Г—Б–љ—Л–µ –Љ–µ—А—Л –і—Г–≥ —Б–Њ–≤–њ–∞–і–∞—О—В, —В–∞–Ї –Ї–∞–Ї –≤–њ–Є—Б–∞–љ–љ—Л–µ —Г–≥–ї—Л —А–∞–≤–љ—Л. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Є —А–∞–і–Є—Г—Б—Л —Г —Н—В–Є—Е –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є —А–∞–≤–љ—Л. –Ґ–∞–Ї–Є—Е –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є –Љ–Њ–ґ–љ–Њ –њ—А–Њ–≤–µ—Б—В–Є —В–Њ–ї—М–Ї–Њ –і–≤–µ, –Є —В–Њ–ї—М–Ї–Њ —В–∞–Ї, —З—В–Њ–±—Л —Ж–µ–љ—А—Л –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є —А–∞—Б–њ–Њ–ї–∞–≥–∞–ї–Є—Б—М –њ–Њ —А–∞–Ј–љ—Л–µ —Б—В–Њ—А–Њ–љ—Л –Њ—В –љ–∞—И–µ–є —Е–Њ—А–і—Л. –Р –≤ –љ–∞—И–µ–Љ —Б–ї—Г—З–∞–µ —Ж–µ–љ—В—А—Л —П–≤–љ–Њ –ї–µ–ґ–∞—В –њ–Њ –Њ–і–љ—Г —Б—В–Њ—А–Њ–љ—Г. –Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б–Њ–≤–њ–∞–і–∞—О—В, —В.–µ. —Г–≥–ї—Л –њ—А–Є–љ–∞–ґ–ї–µ–ґ–∞—В –Њ–і–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
(2017-03-03 17:13:03) –У–µ–љ—А–Є—Е: –°–Ї–∞–ґ–Є—В–µ –њ–Њ–ґ–∞–ї—Г–є—Б—В–∞, –Ї–∞–Ї –і–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –µ—Б–ї–Є –і–≤–∞ —Г–≥–ї–∞, –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ BDA BCA, –Њ–њ–Є—А–∞—О—В—Б—П –љ–∞ –Њ–і–љ—Г –і—Г–≥—Г –Є —А–∞–≤–љ—Л, —В–Њ –Њ–љ–Є –≤–њ–Є—Б–∞–љ—Л –≤ –Њ–і–љ—Г –Є —В—Г –ґ–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М? –Я–Њ-–Љ–Њ–µ–Љ—Г —Н—В–Њ –љ–µ –Њ—З–µ–≤–Є–і–љ–Њ.
(2016-12-21 18:50:49) –Ш–љ–љ–∞: –Ф–∞. –Ъ–ї–∞—Б—Б! –Ґ–µ–њ–µ—А—М –њ–Њ–љ—П—В–љ–Њ, —З—В–Њ –Љ–µ—В–Њ–і–Њ–Љ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П –Є–Ј –њ–µ—А–≤–Њ–є –њ—А–Њ–њ–Њ—А—Ж–Є–Є –њ–Њ–ї—Г—З–∞–µ—В—Б—П –≤—В–Њ—А–∞—П. –С–Њ–ї—М—И–Њ–µ —Б–њ–∞—Б–Є–±–Њ.
(2016-12-20 17:00:17) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ш–љ–љ–∞, —В–µ–њ–µ—А—М —П –Т–∞—Б –њ–Њ–љ—П–ї. –ѓ –і–Њ–±–∞–≤–Є–ї –≤ —А–µ—И–µ–љ–Є–µ –њ–∞—А—Г —Б—В—А–Њ–Ї, —З—В–Њ–±—Л –≤—Б–µ —Б—В–∞–ї–Њ –њ—А–∞–≤–Є–ї—М–љ–Њ –Є –њ–Њ–љ—П—В–љ–Њ. –ѓ, –≤–Є–і–Є–Љ–Њ, –Ј—А—П –Њ–њ—Г—Б—В–Є–ї —Н—В–Є –≤—Л—З–Є—Б–ї–µ–љ–Є—П. –°–њ–∞—Б–Є–±–Њ, —З—В–Њ –Њ–±—А–∞—В–Є–ї–Є –љ–∞ —Н—В–Њ –≤–љ–Є–Љ–∞–љ–Є–µ. –Ґ–µ–њ–µ—А—М –≤—Б–µ —Е–Њ—А–Њ—И–Њ?
(2016-12-20 16:34:00) –Ш–љ–љ–∞: –Ґ–Њ –µ—Б—В—М —П –њ–Є—И—Г –Њ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–µ –њ–Њ–і–Њ–±–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –Р–Т–Ю –Є –Ф–°–Ю, –≥–і–µ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –≤—В–Њ—А–Њ–є –њ—А–Є–Ј–љ–∞–Ї –њ–Њ–і–Њ–±–Є—П. –Ш–Ј –њ–Њ–ї—Г—З–µ–љ–љ–Њ–є –њ—А–Њ–њ–Њ—А—Ж–Є–Є –љ–µ–ї—М–Ј—П —Б–і–µ–ї–∞—В—М –≤—Л–≤–Њ–і, —З—В–Њ —Б—В–Њ—А–Њ–љ—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –Р–Т–Ю –Є –Ф–°–Ю –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ—Л.
(2016-12-20 16:27:01) –Ш–љ–љ–∞: –†–µ—З—М –Є–і—С—В –Њ –≤—В–Њ—А–Њ–Љ –њ—А–Є–Ј–љ–∞–Ї–µ, –Ї–Њ–≥–і–∞ –і–Њ–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П –њ–Њ–і–Њ–±–Є–µ –≤—В–Њ—А–Њ–є –њ–∞—А—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –њ–Њ–ї—Г—З–µ–љ–љ–Њ–є –њ—А–Њ–њ–Њ—А—Ж–Є–Є.–Ш —В—Г—В –Є –љ–µ –њ–Њ–ї—Г—З–∞–µ—В—Б—П —В–Њ–≥–Њ, —З—В–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ—Л.
(2016-12-20 11:41:03) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ш–љ–љ–∞, –њ–Њ –њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г –њ–Њ–і–Њ–±–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤. "–Х—Б–ї–Є –і–≤–∞ —Г–≥–ї–∞ –Њ–і–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —А–∞–≤–љ—Л –і–≤—Г–Љ —Г–≥–ї–∞–Љ –і—А—Г–≥–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —В–Њ —В–∞–Ї–Є–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є –њ–Њ–і–Њ–±–љ—Л". –Р —Г–ґ–µ –Є–Ј –і–Њ–Ї–∞–Ј–∞–љ–љ–Њ–≥–Њ –њ–Њ–і–Њ–±–Є—П –Љ—Л –Љ–Њ–ґ–µ–Љ —Г—В–≤–µ—А–ґ–і–∞—В—М –Њ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є —Б—В–Њ—А–Њ–љ.
–Э–∞–ґ–Є–Љ–∞–є—В–µ –љ–∞ —Б—Б—Л–ї–Ї–Є –≤ —А–µ—И–µ–љ–Є–Є, —В–Њ–≥–і–∞ –≤—Л —Г–≤–Є–і–Є—В–µ –Љ–∞—В–µ—А–Є–∞–ї—Л –љ–∞ –Ї–Њ—В–Њ—А—Л–µ —П —Б—Б—Л–ї–∞—О—Б—М.
(2016-12-19 19:50:21) –Ш–љ–љ–∞: –Т–Њ –≤—В–Њ—А–Њ–Љ –≤–∞—А–Є–∞–љ—В–µ –Њ—В–љ–Њ—И–µ–љ–Є—П —Б—В–Њ—А–Њ–љ –Ю–Т –Є –Ю–Р, –∞ —В–∞–Ї–ґ–µ –Ю–° –Є –Ю–Ф —А–∞–Ј–≤–µ –Љ–Њ–ґ–љ–Њ –љ–∞–Ј–≤–∞—В—М –Њ—В–љ–Њ—И–µ–љ–Є—П–Љ–Є –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ—Л—Е —Б—В–Њ—А–Њ–љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –Р–Т–Ю –Є –Т–°–Ю? –Ь—Л –ґ–µ –≤–Є–і–Є–Љ, —З—В–Њ –Ю–Т –Є –Ю–Р - —Б—В–Њ—А–Њ–љ—Л –Њ–і–љ–Њ–≥–Њ —В—А–µ—Г–≥.–Р–Т–Ю, —В–∞–Ї –ґ–µ –Є —Б—В–Њ—А–Њ–љ—Л –Ю–° –Є –Ю–Ф - —Б—В–Њ—А–Њ–љ—Л –Њ–і–љ–Њ–≥–Њ —В—А–µ—Г–≥.–Т–°–Ю? –Ъ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –њ—А–Є–≤–µ–і—С–љ–љ–Њ–µ –≤ –Ј–∞–і–∞—З–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –і–Њ–Ї–∞–Ј—Л–≤–∞–µ—В –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В—М —Б—В–Њ—А–Њ–љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –Р–Т–Ю –Є –Т–°–Ю?
(2016-12-17 10:33:42) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Т–ї–∞–і–Є—Б–ї–∞–≤, —В—Г—В —В–Њ–љ–Ї–Є–є –Љ–Њ–Љ–µ–љ—В. –Я—Г—Б—В—М –Р–Т - —Н—В–Њ —Е–Њ—А–і–∞ –Ї–∞–Ї–Њ–є-—В–Њ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є (–Љ—Л –њ–Њ–Ї–∞ –љ–µ –Ј–љ–∞–µ–Љ –Ї–∞–Ї –Њ–љ–∞ –њ—А–Њ—Е–Њ–і–Є—В). –Ґ–∞–Ї–Є—Е –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –Љ–љ–Њ–≥–Њ. –Т—Л–±–µ—А–µ–Љ —В–∞–Ї—Г—О –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, –і–ї—П –Ї–Њ—В–Њ—А–Њ–є —Г–≥–Њ–ї BCA –±—Г–і–µ—В –≤–њ–Є—Б–∞–љ–љ—Л–Љ.–І–µ—А–µ–Ј —В–Њ—З–Ї–Є A, B –Є C –≤—Б–µ–≥–і–∞ –Љ–Њ–ґ–љ–Њ –њ—А–Њ–≤–µ—Б—В–Є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Р —В–∞–Ї –Ї–∞–Ї —Г–≥–Њ–ї BDA —А–∞–≤–µ–љ BCA –Є –Њ–њ–Є—А–∞–µ—В—Б—П –љ–∞ —В—Г –ґ—Г –і—Г–≥—Г, —В–Њ —Г–≥–Њ–ї BDA —В–Њ–ґ–µ –Њ–Ї–∞–ґ–µ—В—Б—П –≤–њ–Є—Б–∞–љ–љ—Л–Љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –њ–Њ–ї—Г—З–Є—В—Б—П, —З—В–Њ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –Њ–њ–Є—Б–∞–љ–∞ –≤–Њ–≥—А—Г–≥ —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
(2016-12-16 14:04:00) –Т–ї–∞–і–Є—Б–ї–∞–≤: –Ф–∞, —П —В–Њ–ґ–µ –љ–µ –њ–Њ–љ–Є–Љ–∞—О –Ї—В–Њ —Б–Ї–∞–Ј–∞–ї —З—В–Њ –Љ—Л –Љ–Њ–ґ–µ–Љ –Њ–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, –љ–∞–і–Њ —Б–љ–∞—З–∞–ї–∞ –і–Њ–Ї–∞–Ј–∞—В—М —З—В–Њ —Б—Г–Љ–Љ–∞ –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л—Е —Г–≥–ї–Њ–≤ 180.
(2016-05-29 12:27:41) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Х–ї–µ–љ–∞, –Т–µ—А—В–Є–Ї–∞–ї—М–љ—Л–µ —Г–≥–ї—Л - —Н—В–Њ —Г–≥–ї—Л –Њ–±—А–∞–Ј–Њ–≤–∞–љ–љ—Л–µ –і–≤—Г–Љ—П –њ–µ—А–µ—Б–µ—З–µ–љ–љ—Л–Љ–Є –њ—А—П–Љ—Л–Љ–Є –Є –љ–∞—Е–Њ–і—П—Й–Є–µ—Б—П –љ–∞–њ—А–Њ—В–Є–≤ –і—А—Г–≥ –і—А—Г–≥–∞. –Я–∞—А–∞–ї–ї–µ–ї—М–љ—Л–µ –њ—А—П–Љ—Л–µ —В—Г—В –≤–Њ–Њ–±—Й–µ –љ–Є –њ—А–Є —З–µ–Љ.
(2016-05-29 11:52:54) –Х–ї–µ–љ–∞: –Т–Њ–њ—А–Њ—Б –њ–Њ 2 –≤–∞—А–Є–∞–љ—В—Г —А–µ—И–µ–љ–Є—П. –Ъ–∞–Ї —Г–≥–ї—Л BOC –Є AOD –Љ–Њ–≥—Г—В –±—Л—В—М –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л–Љ–Є, –µ—Б–ї–Є –Љ—Л –љ–µ –Ј–љ–∞–µ–Љ, —З—В–Њ –Т–° –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ AD?
(2015-04-30 20:46:35) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –°–∞—И–∞, –љ–Є –≤ —Г—Б–ї–Њ–≤–Є–Є, –љ–Є –≤ —А–µ—И–µ–љ–Є–Є –љ–µ—В –љ–Є –Њ–і–љ–Њ–≥–Њ —Б–ї–Њ–≤–∞ –њ—А–Њ —В—А–∞–њ–µ—Ж–Є—О.
(2015-04-30 18:53:49) –°–∞—И–∞: –Р —А–∞–Ј–≤–µ –Љ–Њ–ґ–љ–Њ –њ—А–Њ—Б—В–Њ —В–∞–Ї –≤–Ј—П—В—М –Є –Њ–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –Њ–Ї–Њ–ї–Њ —В—А–∞–њ–µ—Ж–Є–Є. –Т–µ–і—М —З—В–Њ–±—Л –Њ–њ–Є—Б–∞—В—М –љ—Г–ґ–љ–Њ —А–∞–≤–љ–Њ–±–Њ–Ї—Г—О —В—А–∞–њ–µ—Ж–Є—О?