
Укажите номера верных утверждений.
1) Диагонали любого прямоугольника равны.
2) Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
3) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
Рассмотрим каждое утверждение.
1) "Диагонали любого
прямоугольника равны" - это утверждение верно, т.к. является одним из
свойств прямоугольника.
2) "Если в треугольнике есть один острый угол, то этот треугольник остроугольный" - это утверждение неверно, т.к. не соответствует
определению остроугольного треугольника.
3) "Если точка лежит на
биссектрисе угла, то она равноудалена от сторон этого угла". Расстояние от точки до прямой - отрезок, проведенный из данной точки перпендикулярно прямой.
Рассмотрим рисунок.
Треугольники ABD и BCD -
прямоугольные, т.к. AD и DC - расстояние от точки D (расположенной на биссектрисе) до лучей угла. Сторона BD - общая для этих треугольников, /ABD=/CBD, по
определению биссектрисы. Следовательно,
синусы этих углов тоже равны.
По
определению синуса, sin(ABD)=sin(CBD)=AD/BD=CD/BD, следовательно AD=CD. Т.е. это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
 Лестница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
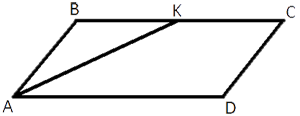 Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
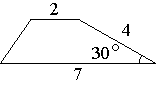 Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7.
Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7.
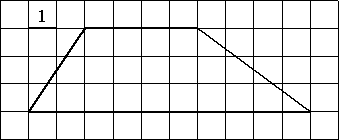 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Комментарии: