
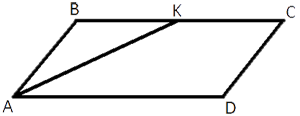 Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
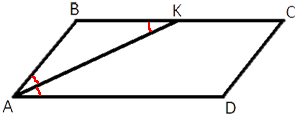 Стороны AD и BC параллельны по
определению параллелограмма.
Стороны AD и BC параллельны по
определению параллелограмма.
Тогда АК мы можем рассмотривать как секущую.
Тогда ∠DAK=∠BKA (так как они
накрест-лежащие).
ВК - вдвое меньше BC (т.к. К - середина).
AB тоже вдвое меньше BC (по условию).
Следовательно, BK=AB, т.е. треугольник ABK равнобедренный.
Тогда, по свойству равнобедренного треугольника, ∠BAK=∠BKA.
Получается, что ∠BAK=∠BKA=∠DAK.
Т.е. AK - биссектрисса.
Поделитесь решением
Присоединяйтесь к нам...
 На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
 В треугольнике ABC известно, что ∠BAC=64°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
В треугольнике ABC известно, что ∠BAC=64°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
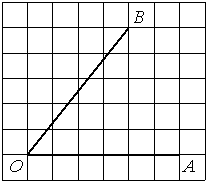 Найдите тангенс угла AOB, изображённого
на рисунке.
Найдите тангенс угла AOB, изображённого
на рисунке.
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
 Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 15, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 15, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Комментарии: