
 Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
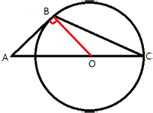 OC является радиусом окружности R, AO=AC-OC.
OC является радиусом окружности R, AO=AC-OC.
Проведем отрезок BO. BO - так же является радиусом окружности. AB -
касательная к окружности, следовательно AB перпендикулярен BO (по
свойству касательной).
Значит треугольник ABO -
прямоугольный, тогда по
теореме Пифагора:
AO2=AB2+BO2
(AC-OC)2=AB2+R2
(10-R)2=62+R2
100-20R+R2=36+R2
100-36=20R
R=3,2
D=2R=2*3,2=6,4
Ответ: D=6,4
Поделитесь решением
Присоединяйтесь к нам...
 В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
 В треугольнике два угла равны 46° и 78°. Найдите его третий угол. Ответ дайте в градусах.
В треугольнике два угла равны 46° и 78°. Найдите его третий угол. Ответ дайте в градусах.
 В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
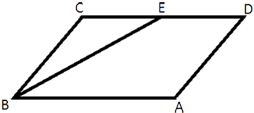 Площадь параллелограмма
ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
Площадь параллелограмма
ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
Комментарии:
(2019-06-03 21:37:20) Администратор: Владимир, AB-касательная по условию задачи, а касательная перпендикулярна радиусу по свойству касательной.
(2019-06-02 11:11:48) владимир: Почему АВ должна быть касательной?
(2019-06-02 11:06:33) владимир: Почему угол ABO(О-центр окружности)является прямым?