Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 7.5, а AB=2.
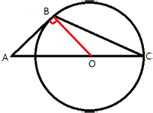Отрезок AC равен сумме отрезков AO и OC, OC - равен радиусу окружности, т.е. 7,5/2=3,75. Найдем AO.
Проведем отрезок BO. BO - так же является радиусом окружности. AB -
касательная к окружности, следовательно AB перпендикулярен BO (по
свойству касательной).
Значит треугольник ABO -
прямоугольный, тогда по
теореме Пифагора:
AO2=AB2+BO2
AO2=22+3,752
AO2=4+14,0625=18,0625
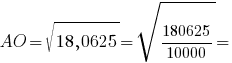
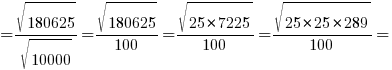
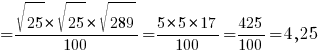
AC=AO+OC=4,25+3,75=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Сторона квадрата равна 6√3. Найдите площадь этого квадрата.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
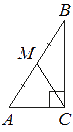В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-02-07 23:55:24) Администратор: Марина, я немного расписал решение...
(2018-02-07 16:48:46) марина: как взять корень из этого числа