
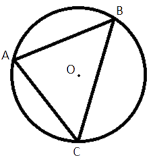 Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Градусная мера всей окружности 360°.
Разделим ее на равные условные части так, чтобы одна дуга имела 3 такие части, вторая дуга 4 части, а третья 11 частей (как у условии задачи). Тогда понятно, что нам нужно 3+4+11 таких частей, итого 18.
Градусная мера каждой части равна 360°/18=20°.
Тогда наша первая дуга имеет градусную меру 20°*3=60°, вторая - 20°*4=80°, третья - 20°*11=220°.
Углы ABC, BCA и CAB -
вписанные в окружность, следовательно, они равны половине градусной меры дуги, на которую опираются, т.е.:
Один угол равен 30°, второй 40°, а третий 110°.
По
теореме о соотношении углов и сторон треугольника: на против меньшей стороны лежит меньший угол. Меньший угол равен 30° (это мы только что вычислили), а меньшая сторона равна 14 (по условию задачи).
По
теореме синусов 14/sin30°=2R
14/0,5=2R
28=2R
R=14
Ответ: R=14
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Синус острого угла A треугольника ABC равен 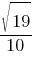 . Найдите CosA.
. Найдите CosA.
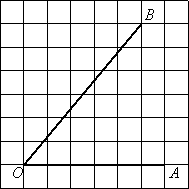 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
 ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
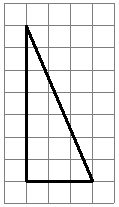 На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Комментарии:
(2018-11-12 21:34:33) Администратор: Аминат, я не вижу вариантов решить проще. Если у Вас есть предложение, то пишите, опубликую под Вашим именем.
(2018-11-10 22:29:24) аминат: как решать попроще
(2016-10-25 21:02:52) Администратор: екатерина, подскажу, треугольник - прямоугольный.
А вообще мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-10-25 17:51:23) екатерина: Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.