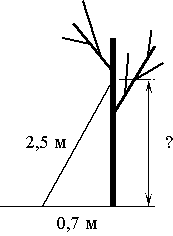
Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Лестница, дерево и земля представляют из себя прямоугольный треугольник. Высоту, на которой находится конец лестницы обозначим как X.
Тогда по теореме Пифагора мы можем записать 2,52=0,72+X2. Отсюда, X2=6,25-0,49, X2=5,76, X=2,4.
Ответ: высота равна 2,4 метра.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: