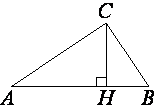
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
По
определению тангенса, tgB=7/2=3,5
Ответ: tgB=3,5.
Поделитесь решением
Присоединяйтесь к нам...
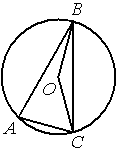Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
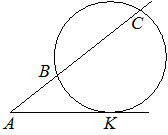Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
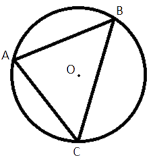Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
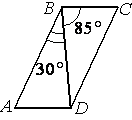Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 85° и 30°. Найдите меньший угол параллелограмма.
В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-21 20:40:29) Администратор: Лена, по определению tg - это отношение ПРОТИВОлежащего катета к ПРИлежащему, поэтому 7/2.
(2015-05-20 16:30:44) Лена: Почему 7/2,а не 2/7?