ОГЭ, Математика.
Геометрия: Задача №84B6C0

Задача №305 из 1087
Условие задачи:

В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.

Решение задачи:

По теореме о сумме углов треугольника: 180°=/A+/B+/C, отсюда /B=180°-/A-/C=180°-30°-50°=100°.
/ABD=/B/2=50° (т.к. BD - биссектриса).
Рассмотрим треугольник BHC, по теореме о сумме углов треугольника получаем 180°=50°+90°+/CBH => /CBH=40°.
Тогда искомый угол /DBH=/B-/ABD-/CBH=100°-50°-40°=10°.
Ответ: /DBH=10°

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №2A7231

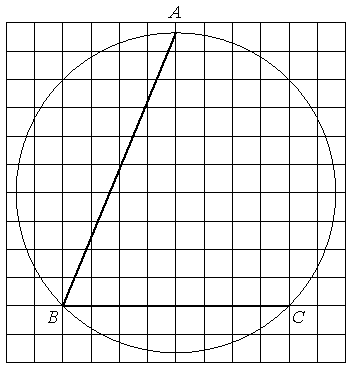Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 74°. Ответ дайте в градусах.

Задача №CD5252

Радиус окружности, описанной около квадрата, равен 16√2. Найдите длину стороны этого квадрата.

Задача №D1939B

Человек, рост которого равен 1,8 м, стоит на расстоянии 16 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).