
Решите уравнение (x2-9)2+(x2-2x-15)2=0.
Вариант №1 (Предложил пользователь Людмила)
Это равенство будет выполняться тогда и только тогда, когда x2-9=0 и
x2-2x-15=0.
Пояснение: оба этих слагаемых возведены в квадрат, следовательно, будут всегда положительные. А сумма двух положительный чисел может быть равна нулю только, когда эти оба числа равны нулю.
Получаем систему уравнений:
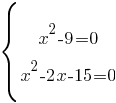
Решим по отдельности каждое уравнение, а одинаковые корни этих уравнений и будут решением системы.
1) x2-9=0
Можно решить это
квадратное уравнение через
дискриминант, но в данном случае выберем путь проще, воспользуемся формулой разность квадратов:
x2-32=0
(x-3)(x+3)=0
Произведение равно нулю, когда один из множителей равен нулю:
x-3=0 => x1=3
x+3=0 => x2=-3
2) x2-2x-15=0
Решим это квадратное уравнение через
дискриминант:
D=(-2)2-4*1*(-15)=4+60=64
x1=(-(-2)+8)/(2*1)=(2+8)/2=5
x2=(-(-2)-8)/(2*1)=(2-8)/2=-3
Для обоих уравнений x=-3 является общим корнем, это и есть решение системы и первоначального уравнения.
Ответ: -3
Поделитесь решением
Присоединяйтесь к нам...
Решите систему уравнений 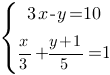
Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 2 часа, вернулись обратно через 6 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 6 км/ч?
Решите неравенство (2x-7)2≥(7x-2)2.
При каком значении x значения выражений 10x-6 и 6x+5 равны?
Городской бюджет составляет 16 млн рублей, а расходы на одну из его статей составили 45%. Сколько рублей потрачено на эту статью бюджета?
Комментарии:
(2017-05-14 18:46:56) Администратор: Людмила, спасибо за подсказку. Я опубликовал Ваш вариант решения от Вашего имени.
(2017-05-13 18:37:51) Людмила: Опять сложное решение. (x2-9)2+(x2-2x-15)2=0 тогда и только тогда, когда x2-9=0 и x2-2x-15=0. Далее решается система этих уравнений