Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
AD для треугольника ABM является и
медианой, и высотой. А это
свойство медианы для равнобедренного треугольника. Следовательно, треугольник ABM -
равнобедренный с основанием BM.
По
определению равнобедренного треугольника AB=AM.
Т.к. BM - медиана для треугольника ABC, следовательно AM=MC (по
определению медианы).
Тогда AC=AM*2. Как мы выяснили ранее AM=AB => AC=AB*2=3*2=6.
Ответ: AC=6.
Поделитесь решением
Присоединяйтесь к нам...
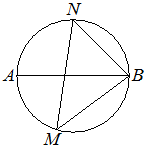На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
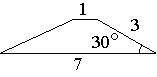Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 1 и 7.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: