
 В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.
∠QNM - является
вписанным в окружность и опирается на дугу QM.
∠QPM тоже является
вписанным в окружность и опирается на дугу QM.
Следовательно, эти углы равны.
∠QNM=∠QPM
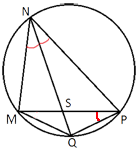 Рассмотрим треугольники NPQ и SPQ.
Рассмотрим треугольники NPQ и SPQ.
∠SQP - общий
∠QNP=∠SPQ
По
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, NQ/QP=QP/SQ
NQ=QP2/SQ=862/43=88=7396/43=172
NS=NQ-SQ=172-43=129
Ответ: NS=129
Поделитесь решением
Присоединяйтесь к нам...
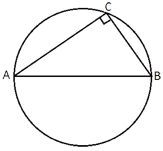 В треугольнике ABC AC=15, BC=5√
В треугольнике ABC AC=15, BC=5√
 Радиус вписанной в квадрат окружности равен 2√2. Найдите радиус окружности, описанной около этого квадрата.
Радиус вписанной в квадрат окружности равен 2√2. Найдите радиус окружности, описанной около этого квадрата.
Какие из следующих утверждений верны?
1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
2) Площадь трапеции равна произведению основания трапеции на высоту.
3) Треугольника со сторонами 1, 2, 4 не существует.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
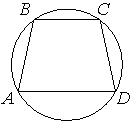 Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
Комментарии:
(2017-05-04 20:09:35) Администратор: NQ/QP=QP/SQ => NQ=QP*QP/SQ=QP^2/SQ
(2017-05-04 16:56:15) : почему в квадрате?
(2015-03-09 17:03:15) Рина: спасибо за красивое решение