
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
Радиус вписанной окружности можно вычислить по формуле R=(AC+CB-AB)/2. Для этого необходимо вычислить длины всех сторон данного треугольника.
Рассмотрим треугольник ABC.
По
определению tgBAC=CB/AC=4/3 => AC=3*CB/4.
По
теореме Пифагора AB2=AC2+CB2
AB2=(3*CB/4)2+CB2
AB2=9*CB2/16+CB2
AB2=25*CB2/16
AB=5*CB/4
Необходимо вычислить CB.
По
теореме о сумме углов треугольника для треугольника ABC:
/ABC=180°-90°-/BAC
Для треугольника BCP:
/ABC=180°-90°-/BCP
Следовательно, /BAC=/BCP.
Рассмотрим треугольник BCP.
По
определению tgBCP=BP/CP=4/3 => CP=3*BP/4.
По
теореме Пифагора CB2=CP2+BP2
CB2=(3*BP/4)2+BP2
CB2=9*BP2/19+BP2
CB2=25*BP2/16
CB=5*BP/4
BP=4*CB/5
r=(BP+CP-CB)/2
2*r=BP+3*BP/4-CB
2*8=7*BP/4-CB
16=7*(4*CB/5)/4-CB
16=(7*4)*CB/(5*4)-CB
16=7*CB/5-CB
16=2*CB/5 |:2
8=CB/5
CB=8*5=40
Вычислив CB, мы можем вычислить AB и AC, указанные выше:
AB=5*CB/4=5*40/4=5*10=50
AC=3*CB/4=3*40/4=3*10=30
R=(AC+CB-AB)/2, тогда получаем:
R=(30+40-50)/2=20/2=10
Ответ: R=10.
Поделитесь решением
Присоединяйтесь к нам...
 Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
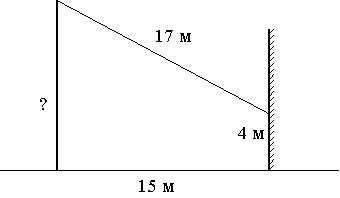 От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
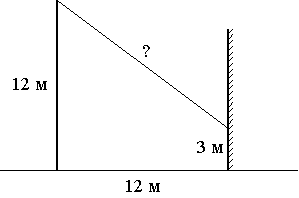 От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.
От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.
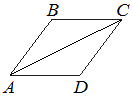 В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
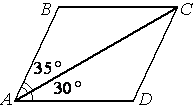 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
Комментарии:
(2015-02-02 18:44:10) Марина: Первый способ решения приводит к верному ответу, хотя используется теорема синусов. Как известно теорема синусов связывает зависимостью стороны, синусы и радиус ОПИСАННОЙ окружности треугольника, что и видно в решении (2R=AB). А нам нужен радиус вписанной окружности.
(2015-02-01 14:19:29) Администратор: Марина, да, Вы правы, изучу как это получилось...
(2015-02-01 11:51:37) Марина: Первый способ решения приводит к верному ответу, хотя используется теорема синусов. Как известно теорема синусов связывает зависимостью стороны, синусы и радиус ОПИСАННОЙ окружности треугольника, что и видно в решении (2R=AB). А нам нужен радиус вписанной окружности.