
 Из вершины прямого угла C треугольника
ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
Из вершины прямого угла C треугольника
ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
Радиус вписанной окружности можно вычислить по формуле R=(AC+CB-AB)/2. Для этого необходимо вычислить длины всех сторон данного треугольника.
Рассмотрим треугольник ABC.
По
определению tgBAC=CB/AC=4/3 => AC=3*CB/4=0,75*CB.
По
теореме Пифагора AB2=AC2+CB2
AB2=(0,75*CB)2+CB2
AB2=1,5625*CB2
AB=1,25*CB
Необходимо вычислить CB.
По
теореме о сумме углов треугольника для треугольника ABC:
/ABC=180°-90°-/BAC
Для треугольника BCP:
/ABC=180°-90°-/BCP
Следовательно, /BAC=/BCP.
Рассмотрим треугольник BCP.
По
определению tgBCP=BP/CP=4/3 => CP=3*BP/4=0,75*BP.
По
теореме Пифагора CB2=CP2+BP2
CB2=(0,75*BP)2+BP2
CB2=1,5625*BP2
CB=1,25*BP
BP=0,8*CB
r=(BP+CP-CB)/2
2*r=BP+0,75*BP-CB
2*8=1,75*BP-CB
16=1,75*0,8*CB-CB
16=0,4*CB
CB=40
Вычислив CB, мы можем вычислить AB и AC, указанные выше:
AB=1,25*CB=1,25*40=50
AC=0,75*CB=0,75*40=30
R=(AC+CB-AB)/2, тогда получаем:
R=(30+40-50)/2=10.
Ответ: R=10.
Поделитесь решением
Присоединяйтесь к нам...
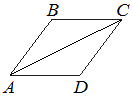 В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 6. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 6. Найдите площадь трапеции.
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 65°. Найдите величину угла OCD.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 65°. Найдите величину угла OCD.
Синус острого угла A треугольника ABC равен 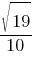 . Найдите CosA.
. Найдите CosA.
 Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 20, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 20, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Комментарии:
(2015-10-13 13:48:55) Администратор: Светлана, да, видимо к этому задача и сводится, но я не могу найти теорему (определение, свойство), в котором бы утверждалось, что в подобных треугольниках отношение сторон равно отношению радиусов вписанных окружностей. А если это нигде не доказано, то принимать это как данность нельзя. Может быть Вы подскажите, где искать?
(2015-10-11 19:13:12) Светлана: проще решить задачу через подобие треугольников:АСВ и СРВ,найти синусА (чрез тангенс найти косинус,затем синус)отношение подобных сторон равно синусу= отношение радиусов