В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
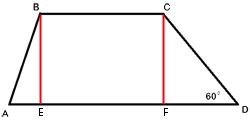Проведем
высоты BE и CF как показано на рисунке.
Рассмотрим треугольник CDF. Он
прямоугольный, т.к. CF-высота.
По
теореме о сумме углов треугольника /FCD=180°-90°-60°=30°.
По
определению синуса sin/FCD=DF/CD=sin30°=1/2
Т.е. DF=CD/2, CD, в свою очередь, по условию задачи равно AD/2, получаем, что DF=AD/4.
BC=AD/2 (по условию задачи)
EF=BC=AD/2 (т.к. BCFE - прямоугольник)
Вычислим AE, AE=AD-DF-EF=AD-AD/4-AD/2=AD/4, т.е. мы получили, что AE=FD
Рассмотрим треугольники ABC и DCF:
BE=CF (т.к. BCFE - прямоугольник)
AE=FD (только что получили)
/AEB=90°=/DFC, тогда по
первому признаку равенства, треугольники ABC и DCF равны.
Следовательно, AB=CD, т.е. наша
трапеция равнобедренная.
AB=CD=2 (по условию задачи), AD=2*CD=2*BC=4 (тоже по условию), BC=CD=2
FD=AD/4=1
По
теореме Пифагора CD2=CF2+FD2
22=CF2+12
CF2=3, CF=√
SABCD=((BC+AD)/2)*CF=((2+4)/2)*√
SABCD=3√
Ответ: SABCD=3√
Поделитесь решением
Присоединяйтесь к нам...
Катеты прямоугольного треугольника равны 20 и 15. Найдите синус наименьшего угла этого треугольника.
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 11°?
Радиус вписанной в квадрат окружности равен 14√
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
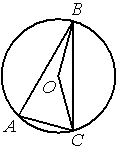Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-09 14:32:31) Администратор: Влад, спасибо за найденную опечатку, исправлено.
(2015-05-07 21:27:18) Влад: Есть ошибка в решении, вроде бы. Написано: "уголAEF = 90 = углуDFC" А должно быть, вроде, уголAEB = 90 = углуDFC