Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
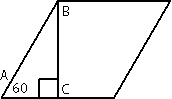Рассмотрим треугольник АВС, этот треугольник
прямоугольный (по условию задачи). /A=60°, следовательно по
теореме о сумме углов треугольника /АВС = 180°-90°-60°=30°. По
свойству прямоугольного треугольника АС=АВ/2=32/2=16. Следовательно вторая половина стороны ромба = 32-16=16. Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: длины обоих отрезков равны 16.
Поделитесь решением
Присоединяйтесь к нам...
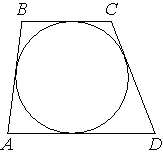Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
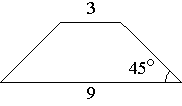В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
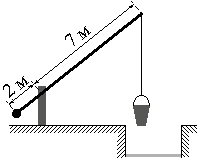На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
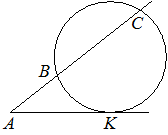Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, BC=32. Найдите AK.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-02-07 23:56:21) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2018-02-07 23:08:46) Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, де: Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?