
На рисунках изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
ГРАФИКИ
А)  Б)
Б)  В)
В) 
КОЭФФИЦИЕНТЫ
1) a<0, c>0
2) a>0, c>0
3) a>0, c<0
В таблице под каждой буквой укажите соответствующий номер.
Коэффициент "а" определяет, куда направлены ветви параболы. Если а<0, то ветви направлены вниз, а если а>0, то вверх.
Поэтому сразу можно сказать, что графику В) соответствуют коэффициенты 1).
Определить знак коэффициента "с" довольно легко, нужно приравнять x к нулю, получится y=a*o2+b*0+c=c. На графике это означает, что если график пересекает ось Y ниже оси X, то с<0, а если выше, то с>0.
Теперь можно сказать, что:
Для графика А) коэффициенты а>0 и c<0 - вариант 3).
Для графика Б) коэффициенты а>0 и c>0 - вариант 2).
| ГРАФИКИ | А) | Б) | В) |
| КОЭФФИЦИЕНТЫ | 3) | 2) | 1) |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=x2+3x-4|x+2|+2 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
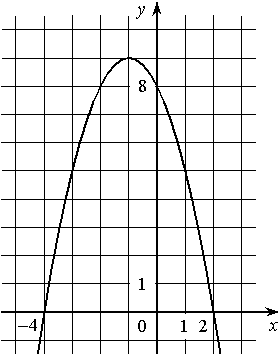 На рисунке изображён график квадратичной функции y=f(x).
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке (-∞;-1]
2) Наибольшее значение функции равно 8
3) f(-4)≠f(2)
Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=x2+0,25 ровно одну общую точку. Постройте этот график и все такие прямые.
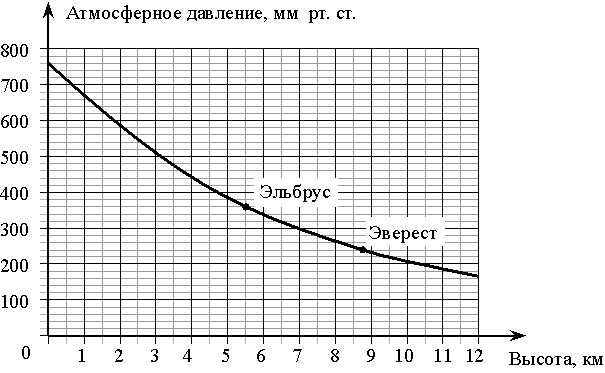 На графике изображена зависимость атмосферного давления от высоты местности над уровнем моря. По горизонтали указана высота над уровнем моря в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?
На графике изображена зависимость атмосферного давления от высоты местности над уровнем моря. По горизонтали указана высота над уровнем моря в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?
Постройте график функции y=|x|x+3|x|-5x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Комментарии: