
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 65°. Найдите величину угла OCD.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 65°. Найдите величину угла OCD.
Рассмотрим треугольник ABO. Этот треугольник
равнобедренный, т.к. ОA и ОB - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OAB=/OBA.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=65°
Ответ: /ODC=65°.
Поделитесь решением
Присоединяйтесь к нам...
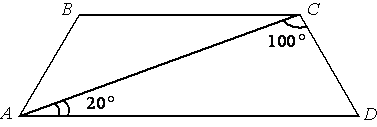 Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
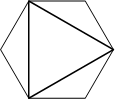 Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
 К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=21, AO=75.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=21, AO=75.
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Комментарии: