В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 65°. Найдите величину угла OCD.
Рассмотрим треугольник ABO. Этот треугольник
равнобедренный, т.к. ОA и ОB - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OAB=/OBA.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=65°
Ответ: /ODC=65°.
Поделитесь решением
Присоединяйтесь к нам...
Сторона AC треугольника ABC проходит через центр окружности. Найдите
∠C, если ∠A=83°. Ответ дайте в градусах.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
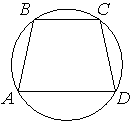Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
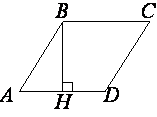Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: