
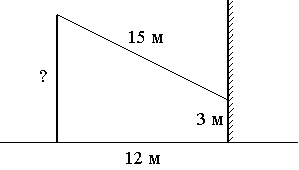
 От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
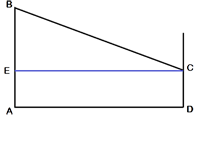 Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD. AECD -
прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD и EA=CD.
Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD. AECD -
прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD и EA=CD.
По
теореме Пифагора BC2=CE2+EB2
152=122+EB2
EB2=225-144
EB2=81
EB=9.
Высота столба = EB+EA=9+3=12.
Ответ: Высота столба - 12 метров.
Поделитесь решением
Присоединяйтесь к нам...
 К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=21, AO=75.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=21, AO=75.
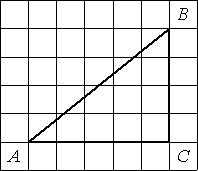 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
 Сторона AC треугольника ABC проходит через центр окружности. Найдите ∠C, если ∠A=30°. Ответ дайте в градусах.
Сторона AC треугольника ABC проходит через центр окружности. Найдите ∠C, если ∠A=30°. Ответ дайте в градусах.
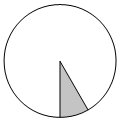 Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
 Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
Комментарии: