
Укажите наименьшее из следующих чисел:
1) √
2) 3√
3) (√
4) √
Чтобы сравнить эти числа, надо привести их к одному виду. Т.е. преобразовать числа так, чтобы число находилось целиком под корнем, или вообще избавиться от корня.
Попробуем оба варианта:
Вариант №1: Заведем все числа под корень:
1) √
2) 3√
3) (√
4) √
Очевидно, что √
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
Какое из данных чисел √0,16, √1,6, √1600?
1) √0,16
2) √1,6
3) √1600
4) все эти числа рациональны
Расстояние от Солнца до Нептуна свет проходит примерно за 252,95 минуты. Найдите приблизительно расстояние от Солнца до Нептуна, ответ округлите до миллионов км. Скорость света равна 300000 км/с.
Найдите значение выражения 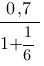
Укажите наименьшее из следующих чисел:
1) √
2) 3√
3) (√
4) √
Известно, что число m отрицательное. На каком из рисунков точки с координатами 0, m, 2m, m2 расположены на координатной прямой в правильном порядке?
1) 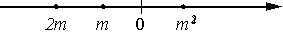
2) 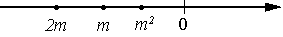
3) 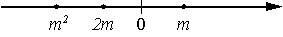
4) 
Комментарии: