
 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
AD для треугольника ABM является и
медианой, и высотой. А это
свойство медианы для равнобедренного треугольника. Следовательно, треугольник ABM -
равнобедренный с основанием BM.
По
определению равнобедренного треугольника AB=AM.
Т.к. BM - медиана для треугольника ABC, следовательно AM=MC (по
определению медианы).
Тогда AC=AM*2. Как мы выяснили ранее AM=AB => AC=AB*2=4*2=8.
Ответ: AC=8.
Поделитесь решением
Присоединяйтесь к нам...
 Сторона равностороннего треугольника равна 2√
Сторона равностороннего треугольника равна 2√
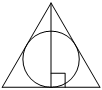 Радиус окружности, вписанной в равносторонний треугольник, равен 12. Найдите высоту этого треугольника.
Радиус окружности, вписанной в равносторонний треугольник, равен 12. Найдите высоту этого треугольника.
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
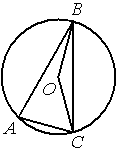 Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25°. Найдите величину угла BOC. Ответ дайте в градусах.
Комментарии: