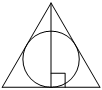
Радиус окружности, вписанной в равносторонний треугольник, равен 12. Найдите высоту этого треугольника.
Из
четвертого свойства равностороннего треугольника найдем его сторону:
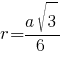
6r=a√3
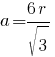
По второму свойству равностороннего треугольника:
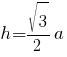
Подставляем значение "a":
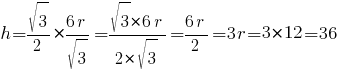
Ответ: 36
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали любого прямоугольника делят его на 4 равных треугольника.
3) Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса.
Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
В треугольнике ABC угол C равен 90°, BC=6, sinA=0,6. Найдите AB.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: