
 Боковая сторона равнобедренного треугольника равна 10, а основание равно 12. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 10, а основание равно 12. Найдите площадь этого треугольника.
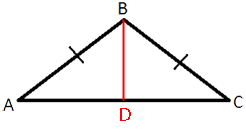 Площадь треугольника равна a*h/2, где h -
высота треугольника, а - сторона треугольника, к которой проведена высота.
Площадь треугольника равна a*h/2, где h -
высота треугольника, а - сторона треугольника, к которой проведена высота.
SABC=AC*BD/2
AD=DC=AC/2=12/2=6 (по
свойству равнобедренного треугольника высота является
медианой)
Тогда, по
теореме Пифагора:
AB2=BD2+AD2
102=BD2+62
100=BD2+36
BD2=64
BD=8
SABC=AC*BD/2=12*8/2=48
Ответ: SABC=48
Поделитесь решением
Присоединяйтесь к нам...
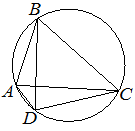 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
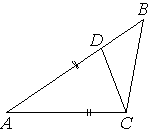 Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника есть центр симметрии.
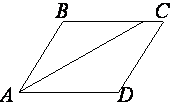 Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
 В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
Комментарии:
(2022-05-12 09:27:42) : квадрат со стороной 8 см описан около окружности. найдите площадь прямоугольного треугольника с острым углом 30, вписанного в данную окружность
(2014-05-17 14:33:39) Администратор: Танюшка, спасибо, хорошее логичное решение. Опубликуем в скором времени.
(2014-05-17 14:29:36) танюшка: Можно решить через теорему Герона. Боковые стороны равны между собой и равны 10.Находим полупериметр: р=(10+10+12)/2=16.Подставляем данные в формулу: S=√16(16-10)*(16-10)*(16-12); S=√64*36 ; S=8*6=48