
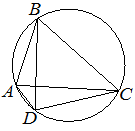
 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
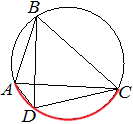 ∠ABC является вписанным углом и опирается на дугу ADC (красная).
∠ABC является вписанным углом и опирается на дугу ADC (красная).
Следовательно, по теореме о вписанном угле, градусная мера дуги ADC равна 70°*2=140°
∠CAD тоже является вписанным углом и опирается на дугу DC.
Следовательно, по теореме о вписанном угле, градусная мера дуги DC равна 49°*2=98°
Тогда легко вычислить градусную меру дуги AD:
140°-98°=42°
Искомый ∠ABD тоже является вписанным углом и опирается на дугу AD.
Следовательно, по теореме о вписанном угле, угол ABD равен:
42°/2=21°
Ответ: 21
Поделитесь решением
Присоединяйтесь к нам...
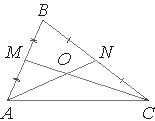 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
 В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
Комментарии: