
 В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
Рассмотрим треугольники AA1C и BB1C.
∠ACA1=∠BCB1, так как они
вертикальные.
∠AA1C=∠BB1C, так как они прямые по условию задачи.
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, по
определению подобных треугольников:
AC/BC=A1C/B1C
Преобразуем это равенство:
AC/A1C=BC/B1C
Рассмотрим треугольники A1CB1 и ABC.
∠ACB=∠A1CB1, так как они
вертикальные.
Тогда, по
второму признаку подобия, данные треугольники
подобны.
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
 Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
 В треугольнике ABC угол C равен 90°, AC=6, tgA=2√
В треугольнике ABC угол C равен 90°, AC=6, tgA=2√
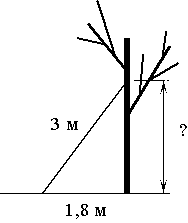 Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Комментарии: