Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника BKP к площади треугольника AMK.
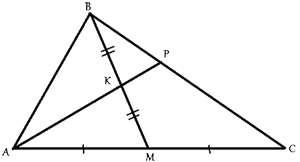По условию задачи ВМ -
медиана треугольника АВС, следовательно, по
свойству медианы, площади треугольников АВМ и ВСМ равны, и равны половине площади треугольника АВС.
SABM=SBCM=(SABC)/2.
В свою очередь, AK является медианой для треугольника АВМ, следовательно, по тому же
свойству медианы
SABК=SAMK=(SABM)/2=(SABC)/4.
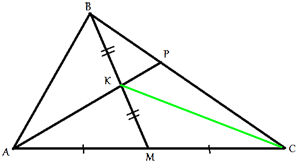Проведем отрезок СК.
СК является
медианой для треугольника СМВ, следовательно,
SCMK=SCKB=(SCMB)/2=(SABC)/4.
Проведем отрезок МЕ, параллельно АР.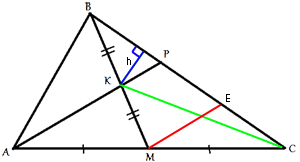
МЕ является
средней линией для треугольника АРС, следовательно (по
теореме о средней линии) СЕ=ЕР. А для треугольника МВЕ
КР является
средней линией, следовательно ВР=ЕР(=СЕ). Т.е. сторона ВС делится на три равные части точками
Р и Е.
Проведем
высоту h, как показано на рисунке. h является общей высотой для треугольников СКВ и BКР.
Выше мы определили, что SCKB=(SABC)/4. Площадь этого же треугольника =(1/2)*h*BC.
SBKP=(1/2)*h*BP=(1/2)*h*(1/3)*ВС=(1/3)*(1/2)*h*BC=(1/3)SCKB=(1/12)SABC.
Следовательно отношение SBKP к SAMK равно (1/12)/(1/4)=1/3.
Ответ: SBKP/SAMK=1/3.
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 16. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Площадь прямоугольного треугольника равна
722√
От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
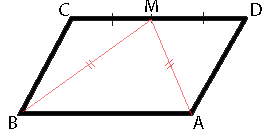В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
Площадь прямоугольного треугольника равна 968√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: