Максим выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 11.
Вероятность любого события равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Найдем сколько всего трехзначных чисел.
Трехзначные числа начинаются с "100" и заканчиваются "999", т.е. всего трехзначных чисел 999-99=900 - это и есть число всех равновозможных несовместных элементарных исходов.
Теперь найдем сколько трехзначных чисел делятся на 11.
Разделим 999 на 11, получим приблизительно 90,81, берем от полученного числа целое значение (не округляем, а берем именно целое). Таким образом от 1 до 999 будет 90 чисел, делящихся на 11. Но нас интересуют только трехзначные числа.
В диапазоне от 1 до 99 чисел, которые делятся на 11, девять (11, 22, 33, .. , 99), т.е. трехзначных чисел, делящихся на 11 всего 90-9=81.
Вероятность того, что выбранное число делится на 11:
P=81/900=9/100=0,09 или 9%
Ответ: P=0,09
Поделитесь решением
Присоединяйтесь к нам...
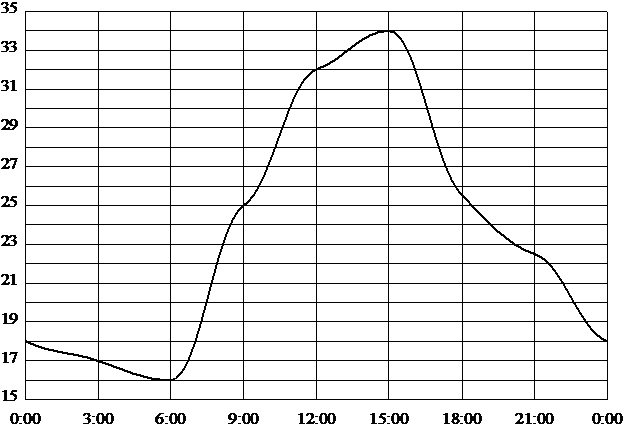На рисунке показано, как изменялась температура на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Сколько часов в первой половине суток температура превышала 25°C?
Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием учебного года, из них 15 с машинами и 5 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Витя. Найдите вероятность того, что Вите достанется пазл с машиной.
Стас выбирает трехзначное число. Найдите вероятность того, что оно делится на 48.
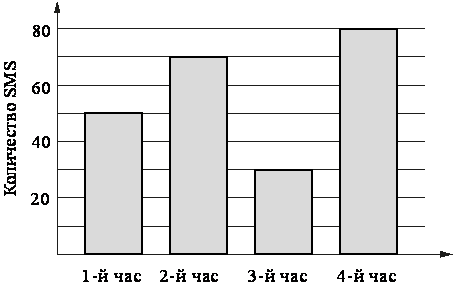На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за первые два часа программы по сравнению с последними двумя часами этой программы.
На диаграмме показан возрастной состав населения Китая.
Сколько примерно человек младше 14 лет проживает в Китае, если население Китая составляет 1,3 млрд человек?
1) около 100 млн
2) около 260 млн
3) около 325 млн
4) около 150 млн
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: