
Укажите номера верных утверждений.
1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.
Рассмотрим каждое утверждение.
1) "Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники
подобны", это утверждение верно по
признаку подобия треугольников.
2) "Смежные углы равны", это утверждение неверно. По
определению, сумма смежных углов равна 180°, поэтому они будут равны только в одном случае, когда равны 90 градусам. В остальных случаях, смежные углы не равны.
3) "Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой", это утверждение верно. Это
свойство равнобедренного треугольника.
Поделитесь решением
Присоединяйтесь к нам...
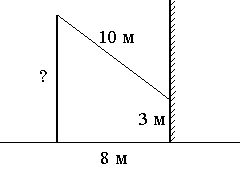 От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
Какие из данных утверждений верны? Запишите их номера.
1) Любой параллелограмм можно вписать в окружность.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
Косинус острого угла A треугольника ABC равен  . Найдите sinA.
. Найдите sinA.
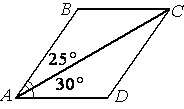 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
 Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
Комментарии: