
Косинус острого угла A треугольника ABC равен  . Найдите sinA.
. Найдите sinA.
Применим основную тригонометрическую формулу:
sin2A+cos2A=1
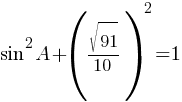
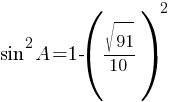
По правилам действий со степенями:
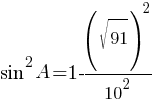
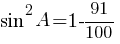
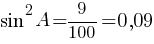
sinA=√0,09=0,3
Ответ: 0,3
Поделитесь решением
Присоединяйтесь к нам...
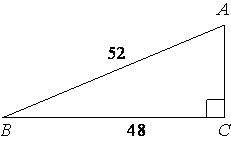 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
 Стороны AC, AB, BC треугольника ABC равны 2√
Стороны AC, AB, BC треугольника ABC равны 2√
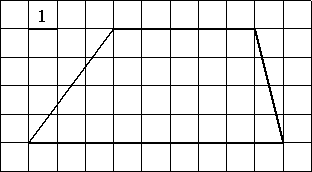 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
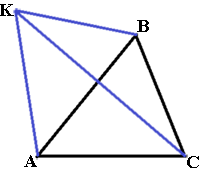
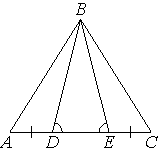 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
Комментарии: