
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
Рассмотрим каждое утверждение.
1) "Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны", это утверждение верно по
свойствам углов.
2)"В любой четырёхугольник можно вписать окружность", это утверждение неверно, т.к. должны выполниться
определенные условия.
3) "Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника", это утверждение верно, по
теореме об описанной окружности.
Поделитесь решением
Присоединяйтесь к нам...
 Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=34.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=34.
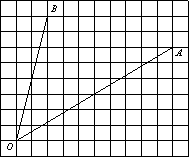 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов остроугольного треугольника равна 180°.
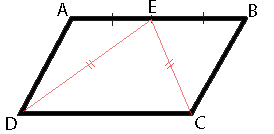 В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
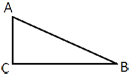 Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 39.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 39.
Комментарии: