Какие из данных утверждений верны? Запишите их номера.
1) Площадь квадрата равна произведению его диагоналей.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Вокруг любого параллелограмма можно описать окружность.
Рассмотрим каждое утверждение.
1) "Площадь квадрата равна произведению его диагоналей". Площадь
квадрата (как и любого
прямоугольника) равна произведению двух соседних сторон, т.е. для квадрата со стороной "а" Sквадрата=a*a=a2.
Диагонали у квадрата равны (по
свойству квадрата), тогда произведение диагоналей будет равно d*d=d2. По
теореме Пифагора получим d2=a2+a2
d2=2*a2
Таким образом получается, что произведение диагоналей квадрата вдвое больше площади квадрата. Т.е. это утверждение неверно
2) "Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны". Т.е. каждая из этих двух прямых образует 4 прямых угла с пересекаемой прямой. Это утверждение верно по
свойству углов.
3) "Вокруг любого
параллелограмма можно описать
окружность". Вокруг четырехугольника можно описать окружность в случае, если сумма противоположных углов равна 180°. А для
параллелограмма это условие может и не выполняться (у параллелограмма нет такого
свойства), следовательно, это утверждение неверно
Поделитесь решением
Присоединяйтесь к нам...
Синус острого угла A треугольника ABC равен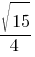 
. Найдите CosA.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
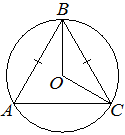Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
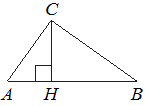На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH.
Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-28 23:56:45) Администратор: Маша, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-05-21 16:10:25) маша: Пло¬щадь тра¬пе¬ции не пре¬вос¬хо¬дит про¬из¬ве¬де¬ния сред¬ней линии на вы¬со¬ту.
(2016-05-29 19:38:58) Яна: Спасибо)