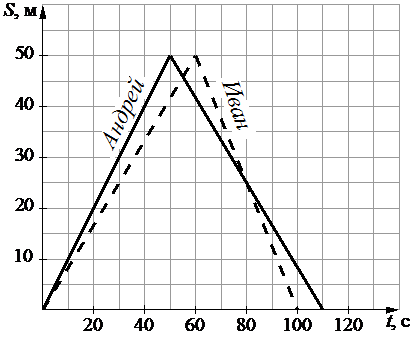
Андрей и Иван соревновались в 50-метровом бассейне на дистанции 100 м. Графики их заплывов показаны на рисунке. По горизонтальной оси отложено время в секундах, а по вертикальной — расстояние пловца от старта в метрах. На сколько секунд обогнал соперника на первой половине дистанции пловец, проплывший её быстрее?
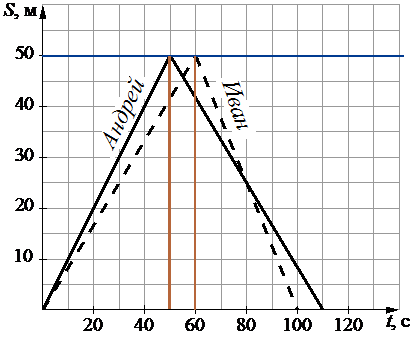Рассмотри график:
Когда прямые графиков возрастают, это означает, что спортсмены удаляются от старта. Когда прямые убывают - это означает, что спортсмены развернулись и возвращаются к старту. Т.е. длина бассейна составляет 50 м. А 100-метровку спортсмены плывут 50 м туда и 50 м обратно.
Следовательно, половина дистанции - это точка на графике, когда происходит "излом" прямой. Значит, смотреть разницу по времени надо именно на этих точках.
По графику видно, что Андрей проплыл половину дистанции за 50 секунд, а Иван - за 60.
60-50=10 секунд.
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
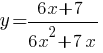
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Андрей и Иван соревновались в 50-метровом бассейне на дистанции 100 м. Графики их заплывов показаны на рисунке. По горизонтальной оси отложено время в секундах, а по вертикальной — расстояние пловца от старта в метрах. На сколько секунд обогнал соперника на первой половине дистанции пловец, проплывший её быстрее?
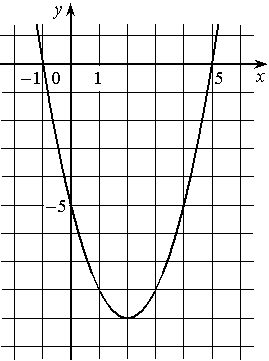На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) f(-1)=f(5)
2) Функция убывает на промежутке [2; +∞)
3) f(x)>0 при x<-1 и при x>5
Постройте график функции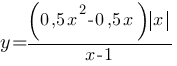 
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
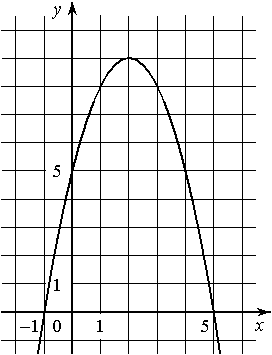На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [2;+∞)
2) ƒ(x)>0 при -1<x<5
3) ƒ(0)<ƒ(4)
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: