
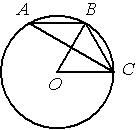
 Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=60°, этот угол является
центральным, соответственно дуга ВC тоже равна 60°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (по теореме о вписанном угле). Соответственно, 60/2=30.
Ответ: /BAC=30°.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
 В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
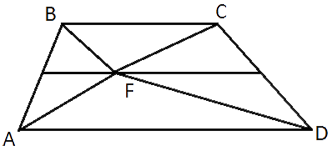 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
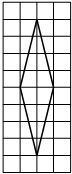 На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
Комментарии: