Катер прошёл от одной пристани до другой, расстояние между которыми по реке равно 48 км, сделал стоянку на 20 мин и вернулся обратно через 5 целых 1/3 ч после начала поездки. Найдите скорость течения реки, если известно, что скорость катера в стоячей воде равна 20 км/ч.
Первое: 5 целых и 1/3 ч. - это 5 часов 20 минут.
Второе: если катер идет по течению реки, то ее скорость складывается со скоростью реки, а если против течения, то вычитается.
Обозначим:
скорость реки - v
Время катера в пути по течению - t1
Время катера в пути против течения - t2
Движение катера по течению (1):
48=(20+v)t1
Движение катера против течения (2):
48=(20-v)t2
При этом, время в пути составило t1+t2, и равно это 5 часов 20 минут минус 20 мин (на стоянку) и равно это 5 часов (3).
(1) t1=48/(20+v)
(2) t2=48/(20-v)
Подставляем в (3):
48/(20+v)+48/(20-v)=5
Приводим к общему знаменателю:
(48(20-v)+48(20+v))/((20+v)(20-v))=5
(960-48v+960+48v)/((20+v)(20-v))=5
1920/(202-v2)=5
1920=5*(400-v2)
1920=2000-5v2
5v2=2000-1920
5v2=80
v2=16
v=4
Ответ: скорость реки равна 4 км/ч
Поделитесь решением
Присоединяйтесь к нам...
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 105 человек. Голоса между кандидатами распределились в отношении 2:5. Сколько голосов получил победитель?
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 105 человек. Голоса между кандидатами распределились в отношении 2:5. Сколько голосов получил победитель?
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв. м, а купить краску можно в одном из двух ближайших магазинов. Цены и характеристики краски даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,6 кг/кв. м | 5 кг | 2400 руб. | 400 руб. |
| 2 | 0,4 кг/кв. м | 4 кг | 2300 руб. | 600 руб. |
Решите уравнение x-6/x=-1.
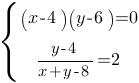
Решите неравенство (x-1)2<√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: