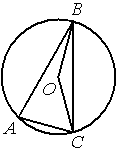
Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=75°, этот угол является
вписанным углом и равен половине градусной меры дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 75°*2=150°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=150°.
Ответ: /BOC=150°.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, sinA=8/9, AC=2√
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
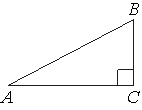В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 16 минут?
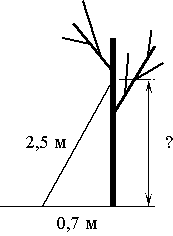Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: