
 В треугольнике ABC угол C равен 90°, sinA=8/9, AC=2√
В треугольнике ABC угол C равен 90°, sinA=8/9, AC=2√
По
определению sinA=BC/AB=8/9
BC=8AB/9
По
теореме Пифагора:
AB2=BC2+AC2
AB2=(8AB/9)2+AC2
AB2=64AB2/81+(2√
AB2-64AB2/81=4*17
(81AB2-64AB2)/81=68
17AB2=81*68
AB2=81*4=324
AB=18
Ответ: AB=18
Поделитесь решением
Присоединяйтесь к нам...
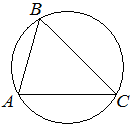 В треугольнике ABC угол C равен 45°, AB=6√
В треугольнике ABC угол C равен 45°, AB=6√
 В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
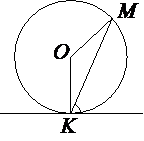 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
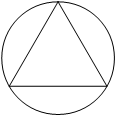 Радиус окружности, описанной около равностороннего треугольника, равен 2√
Радиус окружности, описанной около равностороннего треугольника, равен 2√
 В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
Комментарии: