
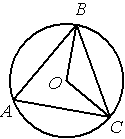
 Точка О – центр окружности, /BAC=60° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=60° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=60°, этот угол является
вписанным углом и равен половине градусной меры дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 60°*2=120°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=120°.
Ответ: /BOC=120°.
Поделитесь решением
Присоединяйтесь к нам...
 Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
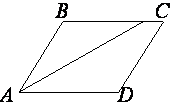 Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам.
2) Не существует прямоугольника, диагонали которого взаимно перпендикулярны.
3) В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.
Какие из следующих утверждений верны?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
Комментарии: