Решите уравнение (4x-8)2(x-8)=(4x-8)(x-8)2.
(4x-8)2(x-8)=(4x-8)(x-8)2
(4x-8)2(x-8)-(4x-8)(x-8)2=0
Вынесем за общую скобку (4x-8)(x-8):
(4x-8)(x-8)((4x-8)-(x-8))=0
(4x-8)(x-8)(4x-8-x+8)=0
(4x-8)(x-8)3x=0 |:3
(4x-8)(x-8)x=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим 3 варианта:
1) 4x-8=0 => x1=2
2) x-8=0 => x2=8
3) x3=0
Ответ: x1=2, x2=8, x3=0
Поделитесь решением
Присоединяйтесь к нам...
Найдите наименьшее значение x, удовлетворяющее системе неравенств
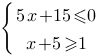
Укажите решение неравенства
2x-x2≤0
1) (-∞;0]∪[2;+∞)
2) [0;+∞)
3) [2;+∞)
4) [0;2]
Решите неравенство 5x-2(2x-8)<-5.
1) (-∞;11)
2) (11;+∞)
3) (-∞;-21)
4) (-21;+∞)
Решите неравенство 2x-x2<0.
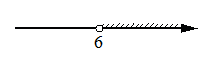
Укажите решение неравенства
x2>36.
1) 
2) 
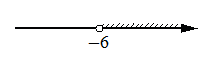
3) 
4) 
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2022-06-22 09:31:03) Вика: (1/4)^x*(8/3)^x ≤ 8/3