Постройте график функции y=x2-6|x|+8. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
y=x2-6x+8, при x≥0
y=x2-6(-x)+8, при x<0
y=x2-6x+8, при x≥0
y=x2+6x+8, при x<0
Рассмотрим и построим график для каждой подфункции на определенном им диапазонах и объединим их.
График обеих подфункций - парабола, при чем, ветви параболы направлены вверх (так как коэффициент "а" больше нуля).
Для первой подфункции (красная):
| X | 0 | 1 | 2 | 3 |
| Y | 8 | 3 | 0 | -1 |
| X | 0 | -1 | -2 | -3 |
| Y | 8 | 3 | 0 | -1 |
Поделитесь решением
Присоединяйтесь к нам...
За 6 минут велосипедист проехал a километров. Сколько километров он проедет за 35 минут, если будет ехать с той же скоростью? Запишите соответствующее выражение.
Закон всемирного тяготения можно записать в виде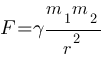 
, где F — сила притяжения между телами (в ньютонах), m1 и m2 — массы тел (в килограммах), r — расстояние между центрами масс тел (в метрах), а γ — гравитационная постоянная, равная 6,67*10-11 Н*м2/кг2. Пользуясь этой формулой, найдите массу тела m1 (в килограммах), если F=4,002 Н, m2=4*109 кг, а r=2 м.
Автобус проехал x километров и израсходовал при этом 27 литров топлива. На сколько километров хватит 80 литров топлива при таких же условиях езды? Запишите соответствующее выражение.
Найдите значение выражения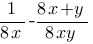 
при x=√
Уравнение x2+px+q=0 имеет корни -5 и 2. Найдите q.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: